Mathematical Model Specification

Mathematical Model Specification#

Mathematical Model Specification for the CADLabs Ethereum Economic Model version v1.1.0.

Overview#

This Mathematical Model Specification articulates the relevant Ethereum validator economics system dynamics as a state-space representation. Given the iterative nature of dynamical systems modelling workflows, we expect to make adjustments to this Mathematical Model Specification as we build and validate the cadCAD model.

Assumptions#

The model implements the official Ethereum Specification wherever possible, but rests on a few default system-level and validator-level assumptions detailed in the model ASSUMPTIONS.md document.

Level of Aggregation#

Although cadCAD technically supports several computational modelling paradigms (e.g. agent-based modelling, population-level modelling, system dynamics modelling, hybrid modelling, etc.) we adopt an aggregate system dynamics lens. Rather than modelling the behaviour of individual agents, we consider what is often called a “representative agent” in economics literature. This allows us to apply aggregation and approximation for groups of agents, or in our case - validators aggregated as validator environments.

Epoch-level Granularity#

Unless specified otherwise in the Mathematical Model Specification, all State Variables, System Metrics, and System Parameters are time-dependent and calculated at per-epoch granularity. For ease of notation, units of time will be assumed implicitly. In the model implementation, calculations can be aggregated across epochs where necessary - for example for performance reasons.

Notation#

The Mathematical Model Specification uses the following notation:

A list / vector of units or in calculations is represented using the matrix symbol: $\begin{bmatrix} x \end{bmatrix}$
A list or vector variable is represented using the vector symbol: $\vec{x}$
A $\Rightarrow$ symbol represents a function that returns a value, ignoring the arguments. For example a Python lambda function lambda x: 1 would be represented as: $\Rightarrow 1$
The superscript $S^+$ is used to define a state transition from state $S$ at the current epoch $e$, to the state at the next epoch $e + 1$
The superscript $S'$ is used to define an individual element to be aggregated in order to get the final state $S$

The following domain notation is used in the Mathematical Model Specification:

$\mathbb{Z}$ - positive and negative integers
$\mathbb{R}$ - positive and negative real numbers
$\mathbb{Z}^+$ - positive integers
$\mathbb{R}^-$ - negative real numbers
etc.

System States#

To create a state-space representation, we first describe the system’s state-space in the form of a set of State Variables. A state-space is a data structure that consists of all possible values of State Variables. The state of the system can be represented as a state vector within the state-space.

For reasons of clarity and comprehensibility we categorize State Variables as follows: ETH State Variables, Validator State Variables, Reward and Penalty State Variables, EIP-1559 State Variables, and System Metric State Variables.

We define the State Variables’ domain, range, and units. The “variable” column values are direct referrences to the cadCAD model code.

ETH State Variables#

Name	Symbol	Domain	Unit	Variable	Description
ETH Price	$P$	$\mathbb{R}^+$	$/\text{ETH}$	`eth_price`	ETH spot price sample (from exogenous process)
ETH Supply	$S$	$\mathbb{R}^+$	$\text{ETH}$	`eth_supply`	ETH supply with inflation/deflation
ETH Staked	$X$	$\mathbb{R}^+$	$\text{ETH}$	`eth_staked`	Total ETH staked (“active balance”) by all active validators

Validator State Variables#

Name	Symbol	Domain	Unit	Variable
# Validators in Activation Queue	$V_{queue}$	$\mathbb{R}^+$	None	`number_of_validators_in_activation_queue`
# Validators	$V$	$\mathbb{R}^+$	None	`number_of_validators`
# Validators Online	$V_{online}$	$\mathbb{R}^+$	None	`number_of_validators_online`
# Validators Offline	$V_{offline}$	$\mathbb{R}^+$	None	`number_of_validators_offline`
Average Effective Balance	$\bar{B}$	$\mathbb{R}^+$	$\text{Gwei}$	`average_effective_balance`
Validator ETH Staked	$\vec{\sigma}$	$\mathbb{R}^+$	$[\text{ETH}]$	`validator_eth_staked`

Reward and Penalty State Variables#

Name	Symbol	Domain	Unit	Variable
Base Reward	$\beta$	$\mathbb{R}^+$	$\text{Gwei}$	`base_reward`
Source Reward	$r_s$	$\mathbb{R}^+$	$\text{Gwei}$	`source_reward`
Target Reward	$r_t$	$\mathbb{R}^+$	$\text{Gwei}$	`target_reward`
Head Reward	$r_h$	$\mathbb{R}^+$	$\text{Gwei}$	`head_reward`
Block Proposer Reward	$r_p$	$\mathbb{R}^+$	$\text{Gwei}$	`block_proposer_reward`
Sync Reward	$r_{sync}$	$\mathbb{R}^+$	$\text{Gwei}$	`sync_reward`
Amount Slashed	$\psi$	$\mathbb{R}^+$	$\text{Gwei}$	`amount_slashed`
Validating Rewards	$R_v$	$\mathbb{R}^+$	$\text{Gwei}$	`validating_rewards`
Whistleblower Rewards	$R_w$	$\mathbb{R}^+$	$\text{Gwei}$	`whistleblower_rewards`
Attestation Penalties	$Z_a$	$\mathbb{R}^+$	$\text{Gwei}$	`attestation_penalties`
Sync Committee Penalties	$Z_{sync}$	$\mathbb{R}^+$	$\text{Gwei}$	`sync_committee_penalties`
Validating Penalties	$Z$	$\mathbb{R}^+$	$\text{Gwei}$	`validating_penalties`
Total Online Validator Rewards	$R_o$	$\mathbb{R}^+$	$\text{Gwei}$	`total_online_validator_rewards`

EIP1559 State Variables#

Name	Symbol	Domain	Unit	Variable
Base Fee per Gas	$f$	$\mathbb{R}^+$	$\text{Gwei/gas}$	`base_fee_per_gas`
Total Base Fee	$F$	$\mathbb{R}^+$	$\text{Gwei}$	`total_base_fee`
Priority Fee per Gas	$t$	$\mathbb{R}^+$	$\text{Gwei/gas}$	`base_fee_per_gas`
Total Priority Fee to Validators	$T_v$	$\mathbb{R}^+$	$\text{Gwei}$	`total_priority_fee_to_validators`
Total Priority Fee to Miners	$T_m$	$\mathbb{R}^+$	$\text{Gwei}$	`total_priority_fee_to_miners`

System Metric State Variables#

We first define System Metrics on the level of the following 7 validator environments, using Numpy array matrix algebra:

DIY Hardware
DIY Cloud
Pool StaaS
Pool Hardware
Pool Cloud
StaaS Full
StaaS Self-Custodied

We then define network-level System Metrics through aggregation.

Validator Environment Level#

The State Variables in this category have the following vector form:

(1)#\[\begin{bmatrix} \text{DIY Hardware}\\ ...\\ \text{StaaS Self-Custodied} \end{bmatrix}\]

Name	Symbol	Domain	Unit	Variable
Validator Revenue	$\vec{K_r}$	$\mathbb{R}$	[$]	`validator_revenue`
Validator Profit	$\vec{K_p}$	$\mathbb{R}$	[$]	`validator_profit`
Validator Revenue Yields	$\vec{Y_r}$	$\mathbb{R}$	$[\%]$	`validator_revenue_yields`
Validator Profit Yields	$\vec{Y_p}$	$\mathbb{R}$	$[\%]$	`validator_profit_yields`
Validator Count Distribution	$\vec{V}$	$\mathbb{R}^+$	$[\%]$	`validator_count_distribution`
Validator Hardware Costs	$\vec{C}_{hardware}$	$\mathbb{R}^+$	[$]	`validator_hardware_costs`
Validator Cloud Costs	$\vec{C}_{cloud}$	$\mathbb{R}^+$	[$]	`validator_cloud_costs`
Validator Third-Party Costs	$\vec{C}_{third-party}$	$\mathbb{R}^+$	$[\%]$	`validator_third_party_costs`
Validator Costs	$\vec{C}$	$\mathbb{R}^+$	[$]	`validator_costs`

Aggregate Network Level#

The above validator-environment-level System Metrics are then aggregated into scalar values to define aggregate network-level system metrics. For example, the validator costs $\vec{C}$ becomes the total network costs $C$ when summed over all 7 validator types.

Name	Symbol	Domain	Unit	Variable
ETH Supply Inflation	$I$	$\mathbb{R}$	$\%$	`supply_inflation`
Total Revenue	$K_r$	$\mathbb{R}$	$	`total_revenue`
Total Profit	$K_p$	$\mathbb{R}$	$	`total_profit`
Total Network Costs	$C$	$\mathbb{R}^+$	$	`total_network_costs`
Total Revenue Yields	$Y_r$	$\mathbb{R}$	$\%$	`total_revenue_yields`
Total Profit Yields	$Y_p$	$\mathbb{R}$	$\%$	`total_profit_yields`

System Inputs#

By defining State Variables we have defined the system’s state-space and with it, system boundaries. System inputs are not dependent on the system’s State Variables. Their logic is defined by Policy Functions in our cadCAD model, and they update the model’s State Variables via State Update Functions.

We describe three environmental processes as System Inputs, updating the ETH Price and ETH Staked State Variables.

Validator Adoption Process & ETH Staked Process#

For the purpose of the model, we define environmental processes for both Validator Adoption and ETH Staked. A certain level of Validator Adoption has an implied ETH Staked value. We use the ETH Staked process to drive the model when performing phase-space analyses of a range of ETH staked values, and the Validator Adoption process when performing time-domain analyses where the validator activation mechanism also comes into play.

The ETH Staked environmental process, represented in the model as a Python lambda function, is called at each epoch with the current run and timestep, and returns the change in ETH staked to update the ETH Staked State Variable during runtime. On the other hand, the Validator Adoption environmental process returns the number of validators being added to the activation queue at each epoch.

For the MVP implementation of our model we assume a representative agent that remains within the system once entered, and we use a monotonically increasing function as a standard adoption model. We also plan the option for the user to manually define validator adoption levels to emulate custom scenarios.

In future model implementations, we could imagine adding feedback loops from State Variables - for instance, capital efficient validators will likely stake and unstake ETH based on the development of validator returns.

ETH Price Process#

For the MVP implementation of our model we use tiered ETH price levels to represent the relevant spectrum of market conditions, similar to Hoban/Borgers’ Economic Model. We also plan the option for the user to manually select ETH price ranges to emulate custom scenarios.

This environmental process, represented in the model as a Python lambda function, is called at each epoch with the current run and timestep, and returns an ETH price sample to update the ETH Price state variable during runtime.

System Parameters#

System Parameters are used as configurable variables in the model’s System Input (Policy Function) and State Update (State Update Function) logic. An example of a parameter would be the BASE_REWARD_FACTOR, used to calculate and update the base reward State Variable.

In a cadCAD model, parameters are lists of Python types that can be swept, or in the case of a stochastic process used to perform a Monte Carlo simulation. For the purpose of experimentation we’ve set defaults, and will sweep parameters within reasonable ranges around these defaults.

Any parameter with the suffix _process can be assumed to be a Python lambda function used to generate a series of values for said parameter, indexed by the run and/or timestep. An illustrative example:

import random

TIMESTEPS = 100
samples = random.sample(range(95, 99), TIMESTEPS + 1)
validator_uptime_process = lambda _run, timestep: samples[timestep] / 100

For reasons of clarity and comprehensibility we categorize parameters as either Ethereum Official Specification, Validator Environment, Validator Performance, or Transaction Pricing System Parameters.

Ethereum Official Specification System Parameters#

All System Parameters in this category use the same uppercase snake-case variable naming seen in the Ethereum Official Specification for easy recognition. See the annotated-spec repository and Benjaminion’s annotated spec for further reference.

Variable	Default Value	Unit
`BASE_REWARD_FACTOR`	`64`	None
`MAX_EFFECTIVE_BALANCE`	`32e9`	$\text{Gwei}$
`EFFECTIVE_BALANCE_INCREMENT`	`1e9`	$\text{Gwei}$
`PROPOSER_REWARD_QUOTIENT`	`8`	None
`WHISTLEBLOWER_REWARD_QUOTIENT`	`512`	None
`MIN_SLASHING_PENALTY_QUOTIENT`	`64`	None
`PROPORTIONAL_SLASHING_MULTIPLIER`	`2`	None
`TIMELY_HEAD_WEIGHT`	`14`	None
`TIMELY_SOURCE_WEIGHT`	`14`	None
`TIMELY_TARGET_WEIGHT`	`26`	None
`SYNC_REWARD_WEIGHT`	`2`	None
`PROPOSER_WEIGHT`	`8`	None
`WEIGHT_DENOMINATOR`	`64`	None
`MIN_PER_EPOCH_CHURN_LIMIT`	`4`	None
`CHURN_LIMIT_QUOTIENT`	`2 ** 16`	None
`BASE_FEE_MAX_CHANGE_DENOMINATOR`	`8`	None
`ELASTICITY_MULTIPLIER`	`2`	None

Validator Environment System Parameters#

Variable	Unit	Description
`validator_percentage_distribution`	$\begin{bmatrix} \% \end{bmatrix}$	The distribution of the total number of validators per validator type. Vector sum is a total of 100%.
`validator_hardware_costs_per_epoch`	$\begin{bmatrix} USD \end{bmatrix}$	The per-epoch costs for DIY hardware infrastructure per validator type
`validator_cloud_costs_per_epoch`	$\begin{bmatrix} USD \end{bmatrix}$	The per-epoch costs for cloud computing resources per validator type
`validator_third_party_costs_per_epoch`	$\begin{bmatrix} \% \end{bmatrix}$	A percentage value of the total validator rewards that goes to third-party service providers as a fee per validator type

Validator Performance System Parameters#

Variable	Default Value	Unit	Description
`validator_uptime_process`	`max(0.98, 2 / 3)`	$\%$	The expected average validator uptime. A combination of validator internet, power, and technical uptime: 99.9 * 99.9 * 98.2. Minimum uptime is inactivity leak threshold of `2/3`, as this model doesn’t model the inactivity leak mechanism.
`slashing_events_per_1000_epochs`	`1`	$\frac{1}{1000}\text{epochs}$	The expected number of validator actions that result in slashing per 1000 epochs

Transaction Pricing System Parameters#

Variable	Default Value	Unit	Description
`base_fee_process`	`25`	$\text{Gwei/gas}$	EIP-1559 transaction pricing base fee burned for each transaction. Default value approximated using average historical gas price - see assumptions doc.
`priority_fee_process`	`2`	$\text{Gwei/gas}$	EIP-1559 transaction pricing priority fee. Default value approximated using average gas price - see assumptions doc.
`gas_target_process`	`15e6`	$\text{Gas}$	The long-term average gas target per block. Simplifying assumption that gas used per block will equal gas target on average over long-term.

State Update Logic#

After defining the model’s state-space in the form of System States, we describe the State Update Logic, represented as cadCAD Policy and State Update Functions (sometimes also called “mechanisms”).

To visualize the State Update Logic, we use a differential specification diagram (also known as a “cadCAD Canvas” at cadCAD Edu). This diagram will accompany the derivation of the Mathematical Model Specification of the model mechanisms.

The model’s cadCAD Canvas / Differential Model Specification is accessible via LucidChart. Below is an illustrative screenshot.

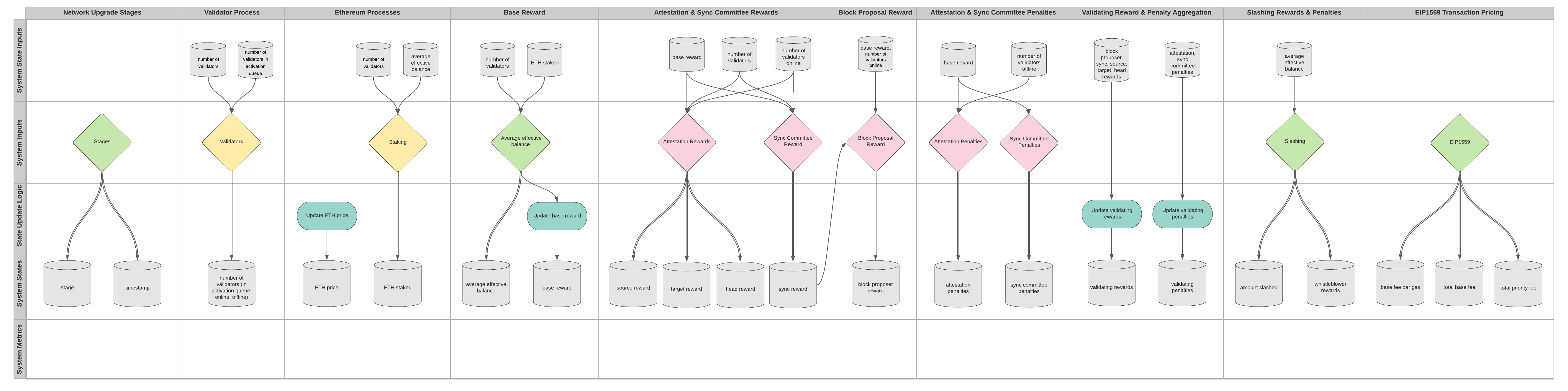
Differential Model Specification

We describe the State Update Logic along the columns of the model’s cadCAD Canvas, also known as “Partial State Update Blocks” (PSUB). One round of execution of these Partial State Update Blocks would represent the state transition from one epoch to the next.

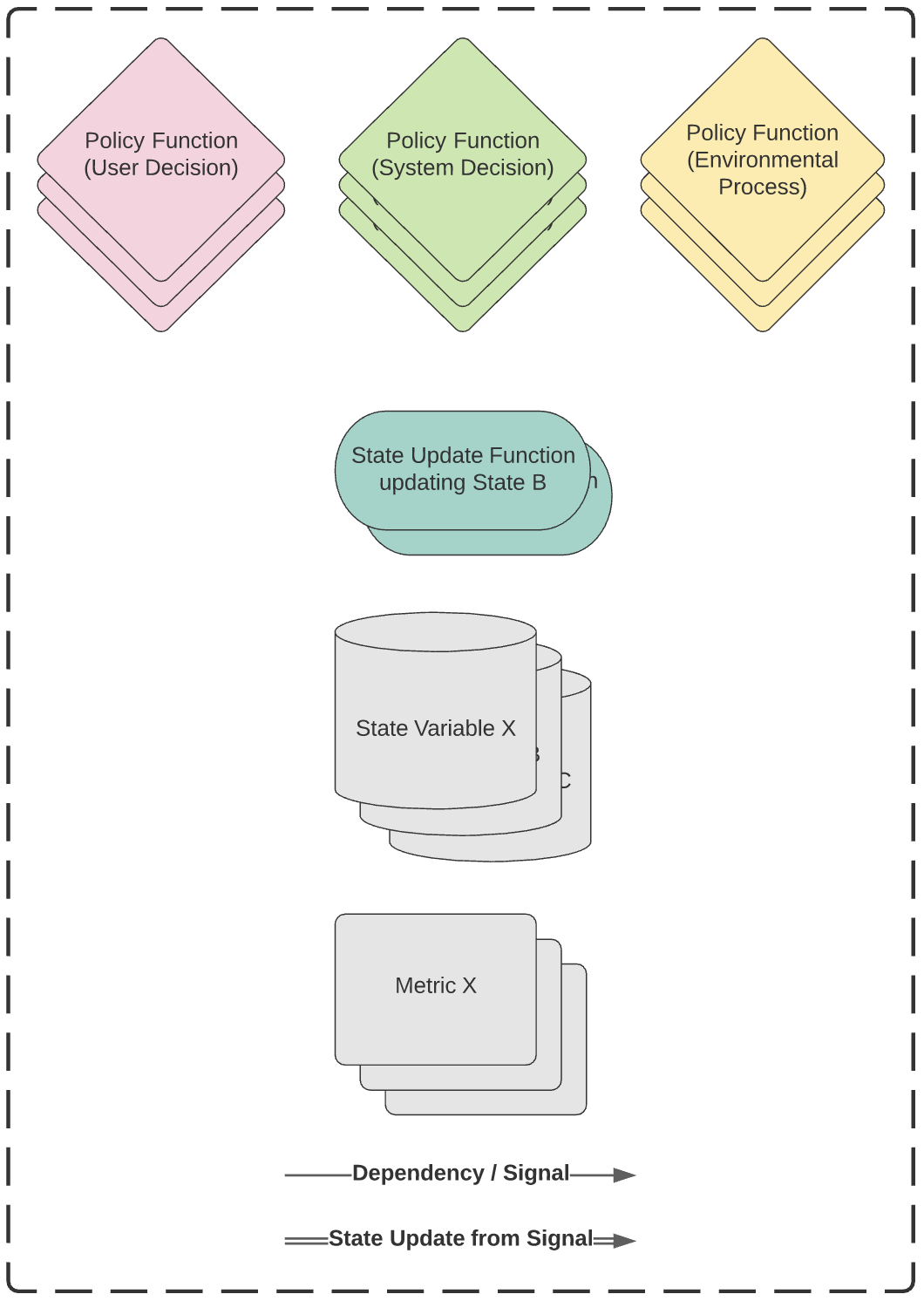
cadCAD Canvas Legend#

Extracts from the cadCAD Canvas have been included for each PSUB below when deriving the Policy and State Update Logic, and the following is the legend included with the cadCAD Canvas:

Constants#

The following constants are used in the derivation of the State Update Logic.

Name	Symbol	Domain	Unit	Variable	Value
Epochs per year	$E_{year}$	$\mathbb{Z}^+$	$\text{epochs}$	`epochs_per_year`	82180
Epochs per day	$E_{day}$	$\mathbb{Z}^+$	$\text{epochs}$	`epochs_per_day`	225

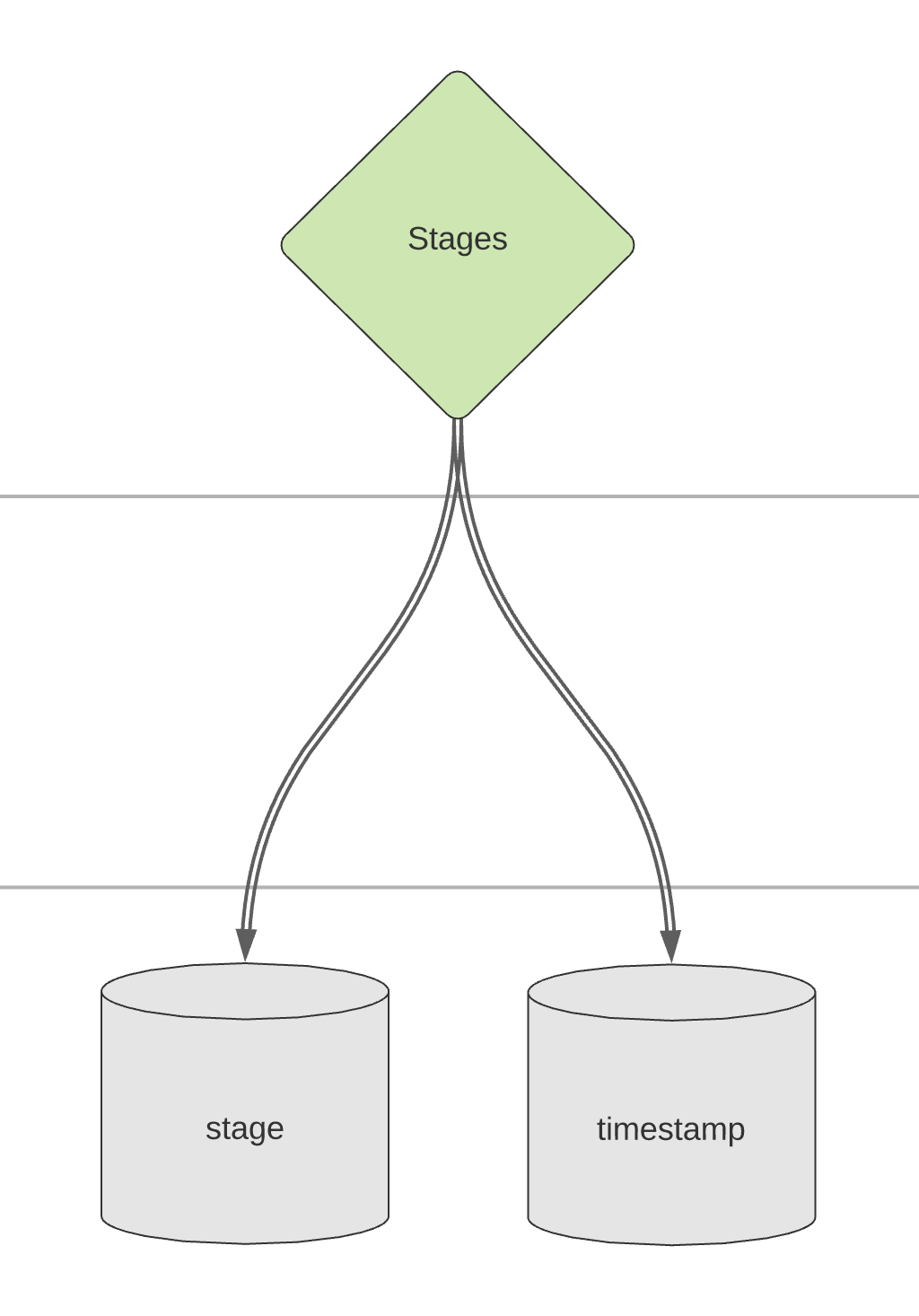
PSUB 1: Network Upgrade Stages#

The Upgrade Stages Policy is essentially a Finite-state Machine that handles the transition from on stage in the Ethereum network upgrade process to the next for time-domain analyses, or simply selecting a single stage for phase-space analyses.

The model has three stages, configured using the Stage Python Enum. The Enum option ALL transitions through all stages in order:

BEACON_CHAIN: Beacon Chain implemented; EIP1559 disabled; POW issuance enabled
EIP1559: Beacon Chain implemented; EIP1559 enabled; POW issuance enabled
PROOF_OF_STAKE: Beacon Chain implemented; EIP1559 enabled; POW issuance disabled

Each stage has a corresponding date, set using the date_{} System Parameters.

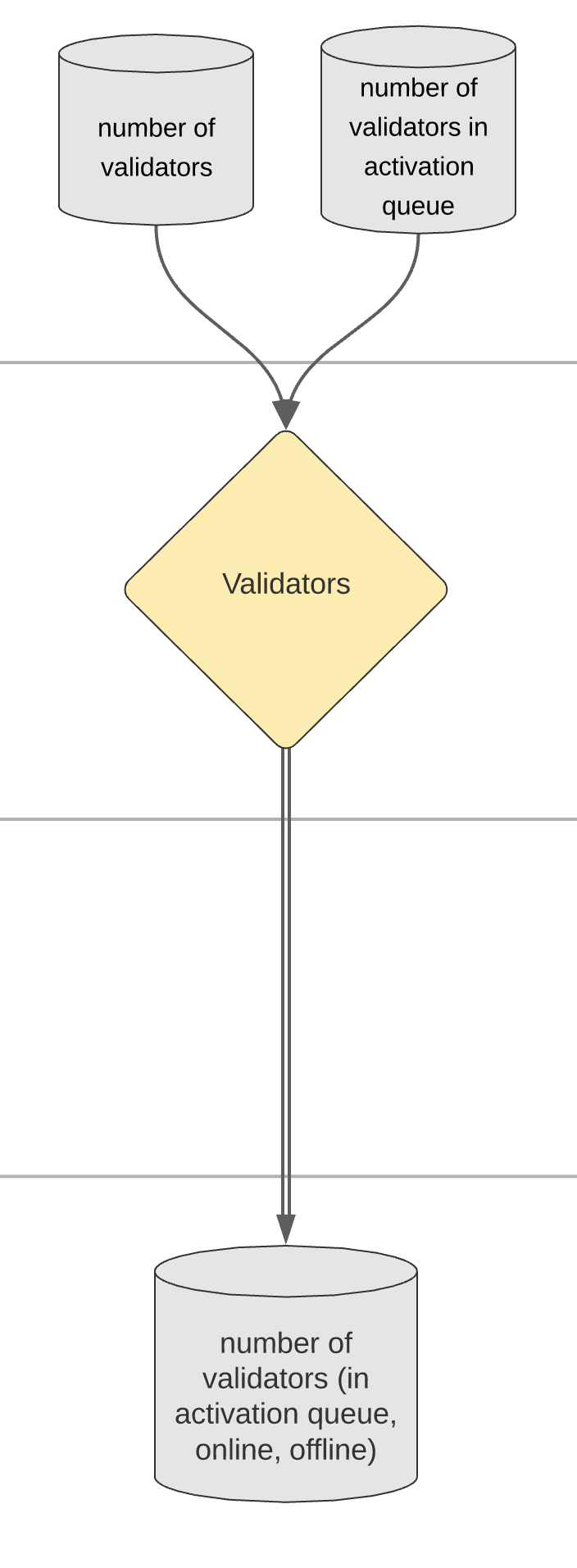
PSUB 2: Validator Process#

Validators that deposit their initial stake first enter into an activation queue before being considered active validators and having their stake as part of the effective balance used when calculating validator rewards and penalties.

(2)#\[\begin{equation} \begin{aligned} \text{churn limit } &= \text{max(MIN_PER_EPOCH_CHURN_LIMIT, $V$ // CHURN_LIMIT_QUOTIENT)}\\ \text{new validators } &= \text{validator_process(run, timestep)} \\ v &= \text{min($V_{queue} +$ new validators, churn limit)}\\ V^+ &= V + v\\ V_{queue}^+ &= V_{queue} - v\\ \end{aligned} \end{equation}\]

The number of validators is equal to the sum of the number of validators online and offline:

(3)#\[\begin{equation} \begin{aligned} V_{online} &= V^+ \times \text{validator uptime} \\ V_{offline} &= V^+ - V_{online} \end{aligned} \end{equation}\]

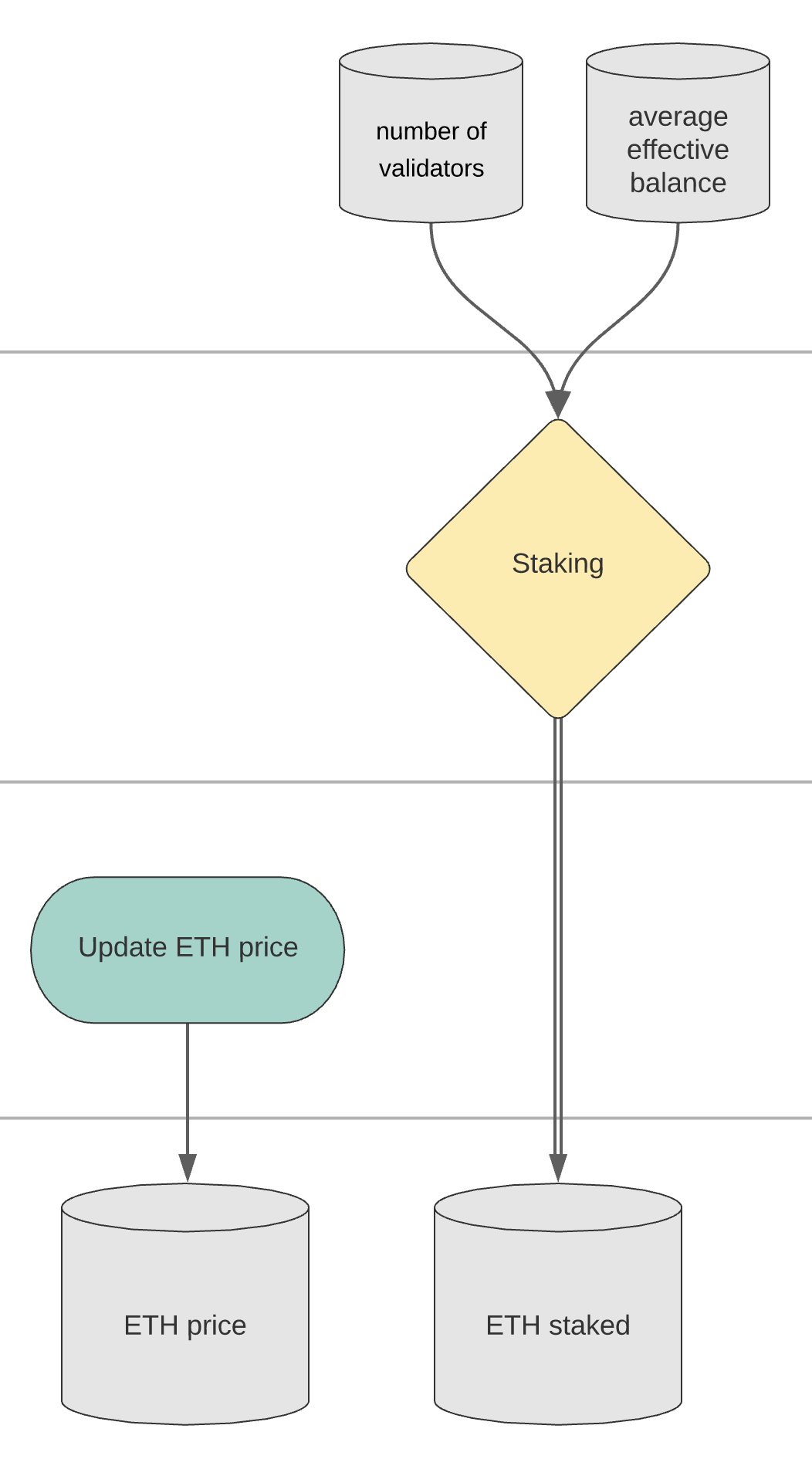
PSUB 3: Ethereum Processes#

The ETH price is driven by an environmental process, defined earlier in the Model Specification, that updates the ETH price at each timestep.

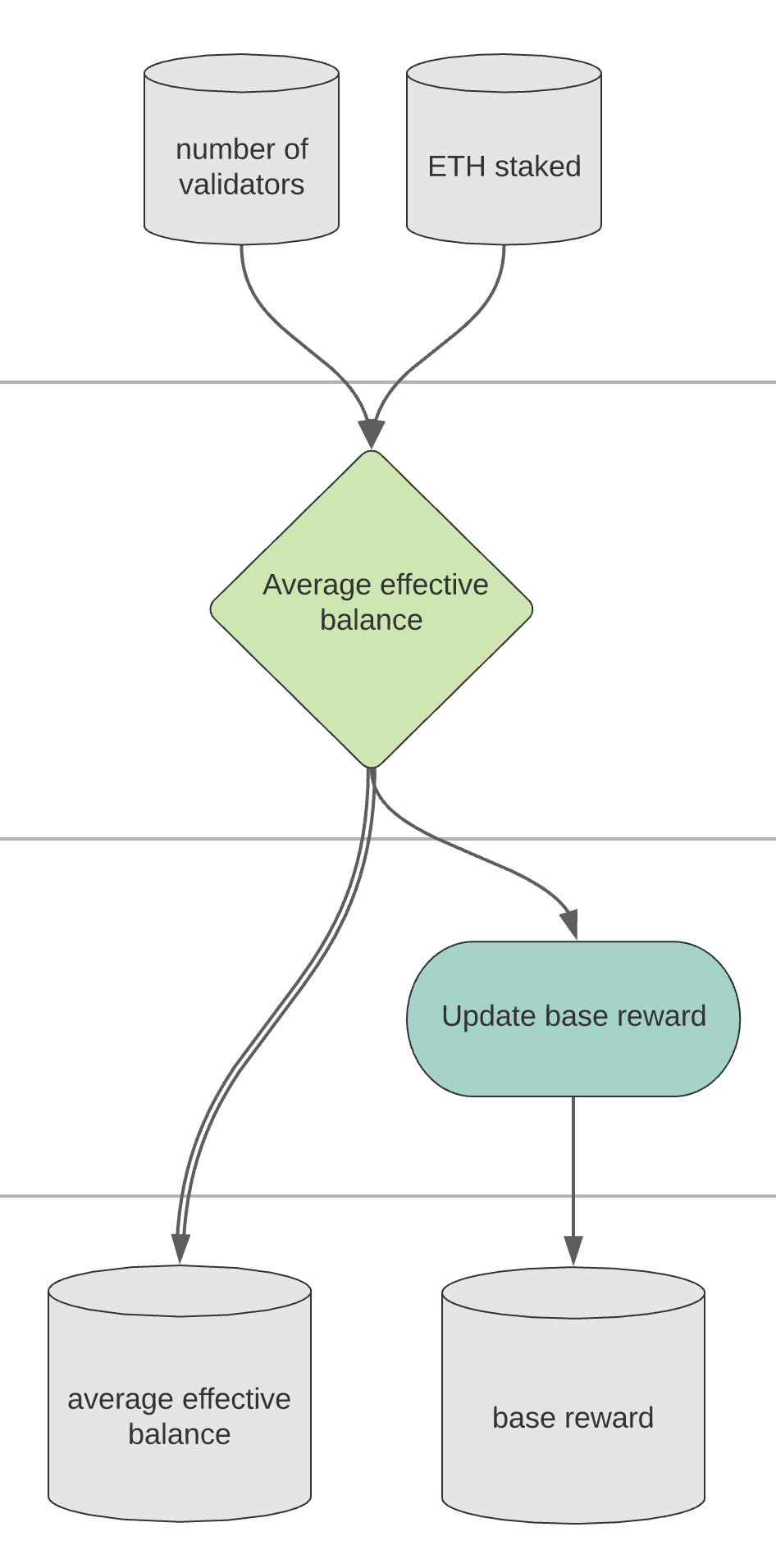
The total ETH staked is the number of activate validators multiplied by the average effective balance in ETH:

\[ X = V \times \frac{\bar{B}}{10^9} \]

PSUB 4: Base Reward#

The following mathematical pseudo-code is used to calculate the aggregate average effective balance of the system:

(4)#\[\begin{equation} \begin{aligned} \bar{B} &= \frac{\text{min(total_effective_balance, MAX_EFFECTIVE_BALANCE $\times V$)}}{V} \\ \text{where}: \\ \text{total_effective_balance} &= X \times 10^9 - X \times 10^9 \quad mod \quad \text{EFFECTIVE_BALANCE_INCREMENT} \\ \end{aligned} \end{equation}\]

The base reward is calculated as the average effective balance multiplied by the ratio of the base reward factor to the square-root of the total ETH staked multiplied by the base rewards per epoch (the higher the ETH Staked, the lower the base reward):

\[ \beta = \frac{\text{min($\bar{B}$, MAX_EFFECTIVE_BALANCE)} \times \text{BASE_REWARD_FACTOR}}{\sqrt{X}} \]

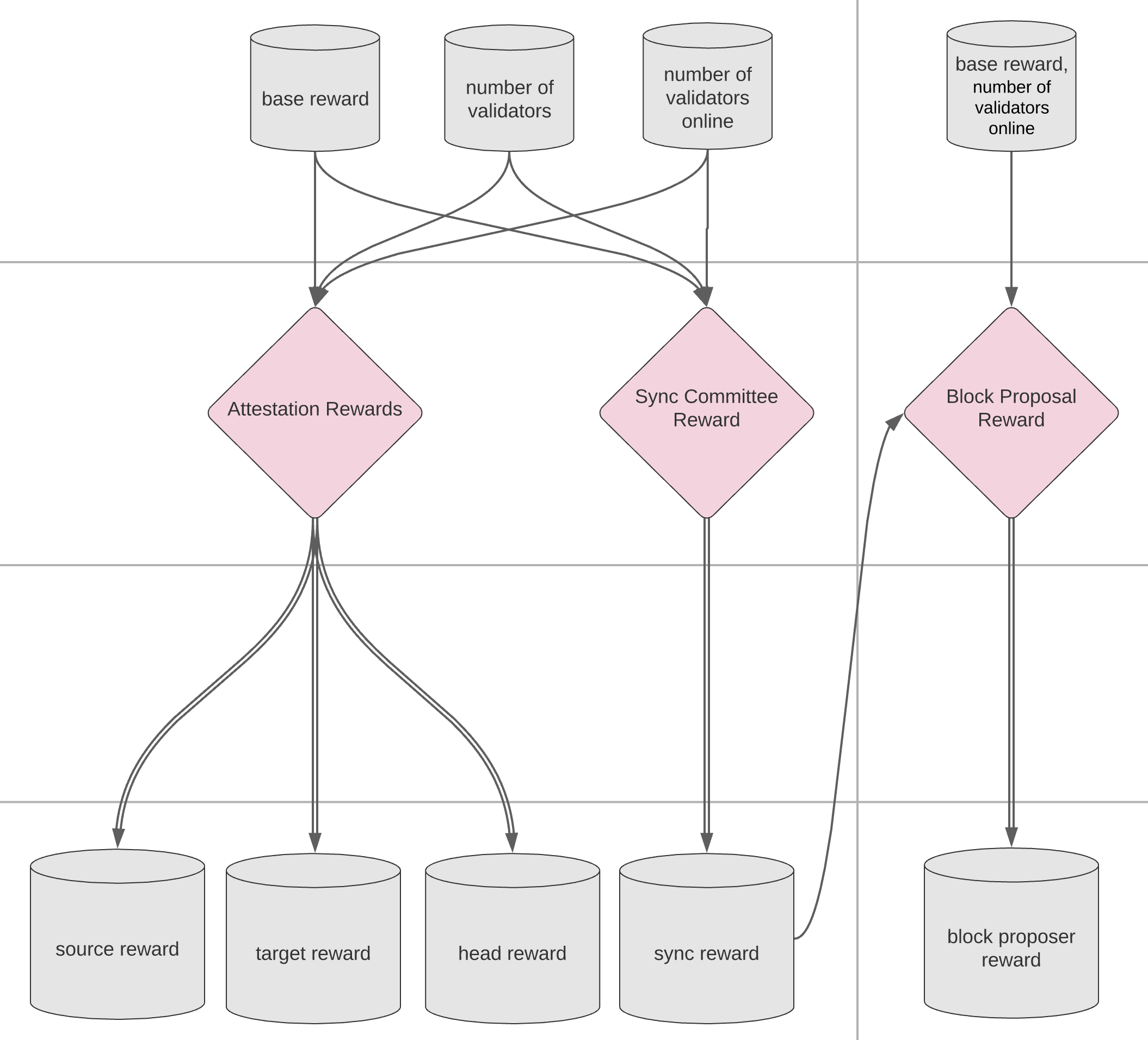
PSUBs 5 & 6: Attestation, Block Proposal & Sync Committee Rewards#

The rewards and penalties from PoS block proposal, attestation, and sync committees, are approximated and aggregated across all validators at each epoch.

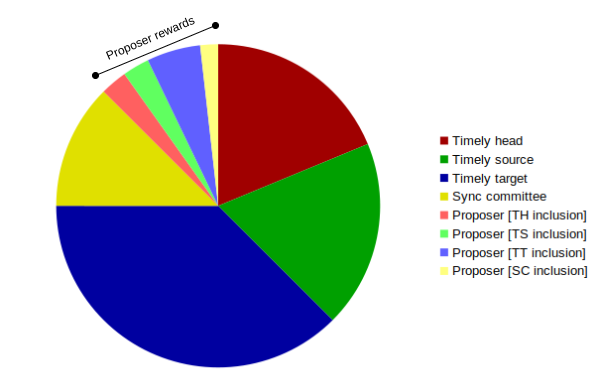
It is useful seeing the rewards as a pie-chart, where the combined rewards are equal to one base reward (see source):

Source, Target, and Head Rewards#

To approximate the source, target, and head vote rewards, it is assumed that all online validators get a source, target, and head vote in time and correctly once per epoch. The calculation for reward per epoch is the same, replacing the TIMELY_SOURCE_WEIGHT with the appropriate reward weight:

(5)#\[\begin{equation} \begin{aligned} r_s &= \frac{\text{TIMELY_SOURCE_WEIGHT}}{\text{WEIGHT_DENOMINATOR}} \times \beta \qquad &(\text{proportion of base reward})\\ &\times \frac{V_{online}}{V} \qquad &\text{(scale by proportion of online valdiators)}\\ &\times V_{online} \qquad &\text{(aggregation over all online validators)}\\ \end{aligned} \end{equation}\]

Sync Committee Reward#

(6)#\[\begin{equation} \begin{aligned} r_{sync} &= \frac{\text{SYNC_REWARD_WEIGHT}}{\text{WEIGHT_DENOMINATOR}} \times \beta \times V \qquad &(\text{proportion of total base rewards})\\ &\times \frac{V_{online}}{V} \qquad &\text{(scale by proportion of online valdiators)}\\ \end{aligned} \end{equation}\]

Block Proposer Reward#

(7)#\[\begin{equation} \begin{aligned} r_p &= \beta \times \text{(W_s + W_t + W_h)} \\ &\times V_{online} \\ &\times \frac{1}{(W_d - W_p) * W_d // W_p} \qquad &(\text{normalize by the sum of weights so that}\\ & \qquad &\text{proposer rewards are 1/8th of base reward})\\\\ &+ r_{sync} \times W_p // (W_d - W_p) \qquad &(\text{add block proposer reward for}\\ & \qquad &\text{including sync committee attestations})\\ \text{where:} \\ W_d &= \text{WEIGHT_DENOMINATOR}\\ W_p &= \text{PROPOSER_WEIGHT}\\ W_s &= \text{TIMELY_SOURCE_WEIGHT}\\ W_t &= \text{TIMELY_TARGET_WEIGHT}\\ W_h &= \text{TIMELY_HEAD_WEIGHT}\\ \end{aligned} \end{equation}\]

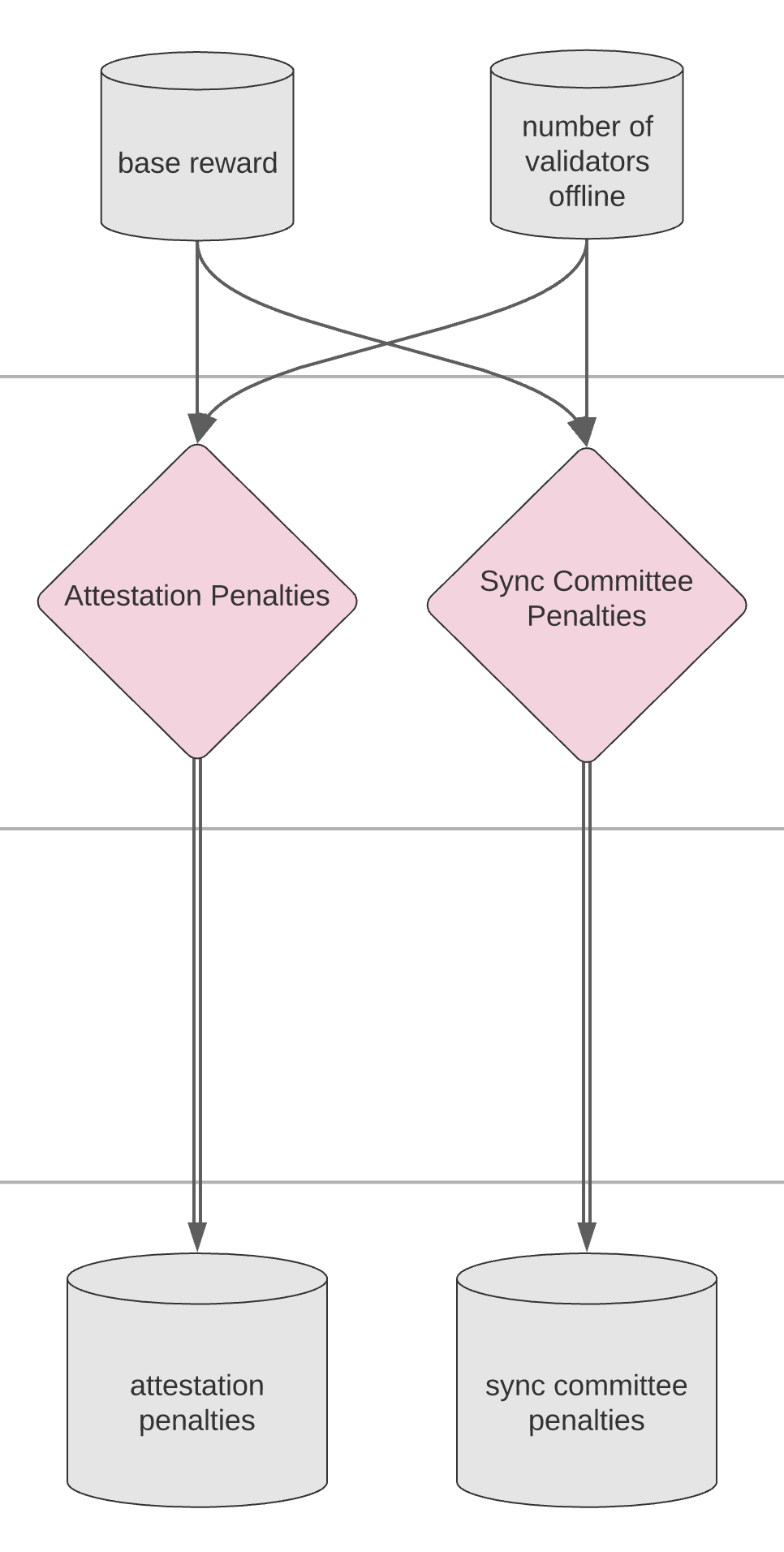
PSUB 7: Attestation & Sync Committee Penalties#

Attestation penalties#

(8)#\[\begin{equation} \begin{aligned} Z_a &= \frac{W_s + W_t + W_h}{\text{WEIGHT_DENOMINATOR}} \times \beta \qquad &(\text{proportion of base reward}) \\ &\times V_{offline} \qquad &(\text{aggregated over all offline validators})\\ \text{where:} \\ W_s &= \text{TIMELY_SOURCE_WEIGHT} \\ W_t &= \text{TIMELY_TARGET_WEIGHT} \\ W_h &= \text{TIMELY_HEAD_WEIGHT} \\ \end{aligned} \end{equation}\]

Sync committee penalties#

It is assumed that all offline validators are penalized for not attesting to the source, target, and head:

(9)#\[\begin{equation} \begin{aligned} Z_s &= \frac{W_{sync}}{\text{WEIGHT_DENOMINATOR}} \times \beta \times V \qquad &(\text{proportion of total base rewards}) \\ &\times \frac{V_{offline}}{V} \qquad &(\text{scaled by % of offline validators}) \\ \text{where:} \\ W_{sync} &= \text{SYNC_REWARD_WEIGHT} \end{aligned} \end{equation}\]

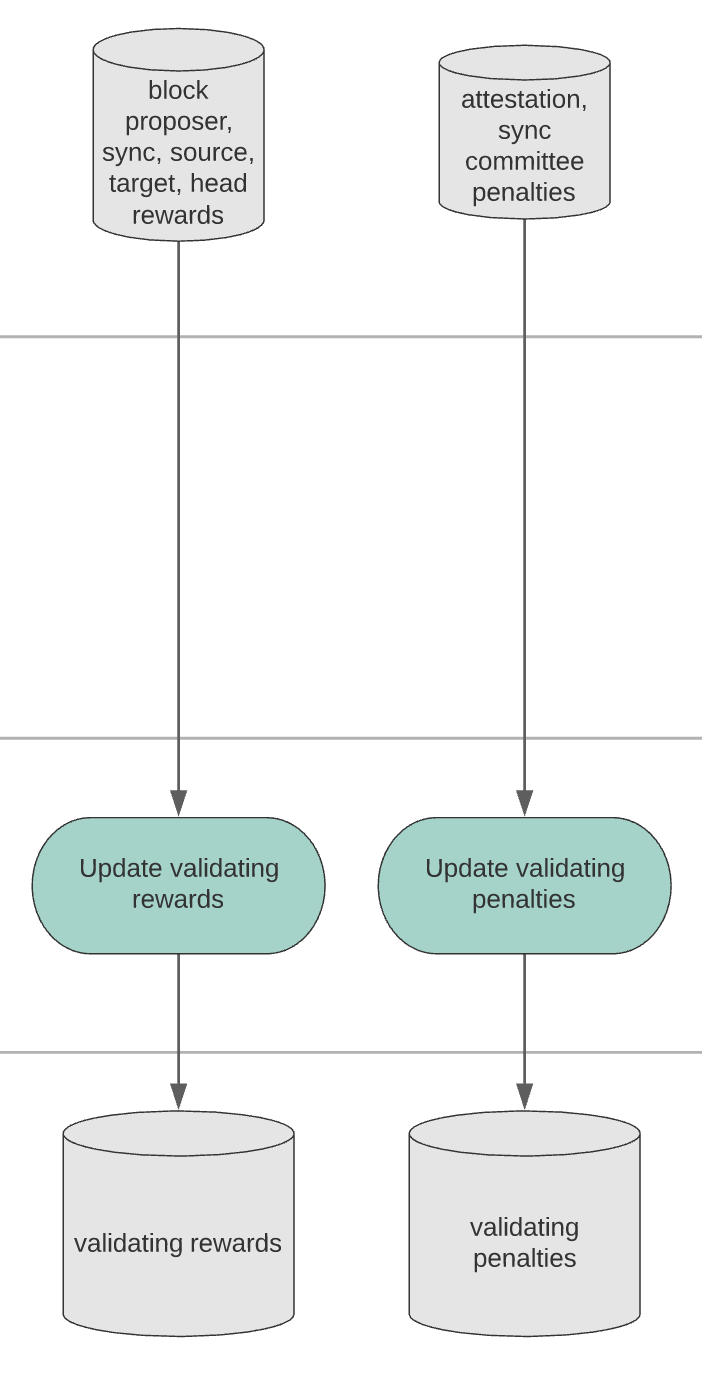
PSUB 8: Validating Reward & Penalty Aggregation#

Validating Rewards#

The total validating rewards is calculated as the sum of all validator reward State Variables:

\[ R_v = r_p + r_s + r_t + r_h + r_{sync} \]

Validating Penalties#

The total validating penalties is the sum of attestation and sync-committee penalties:

\[ Z = Z_a + Z_{sync} \]

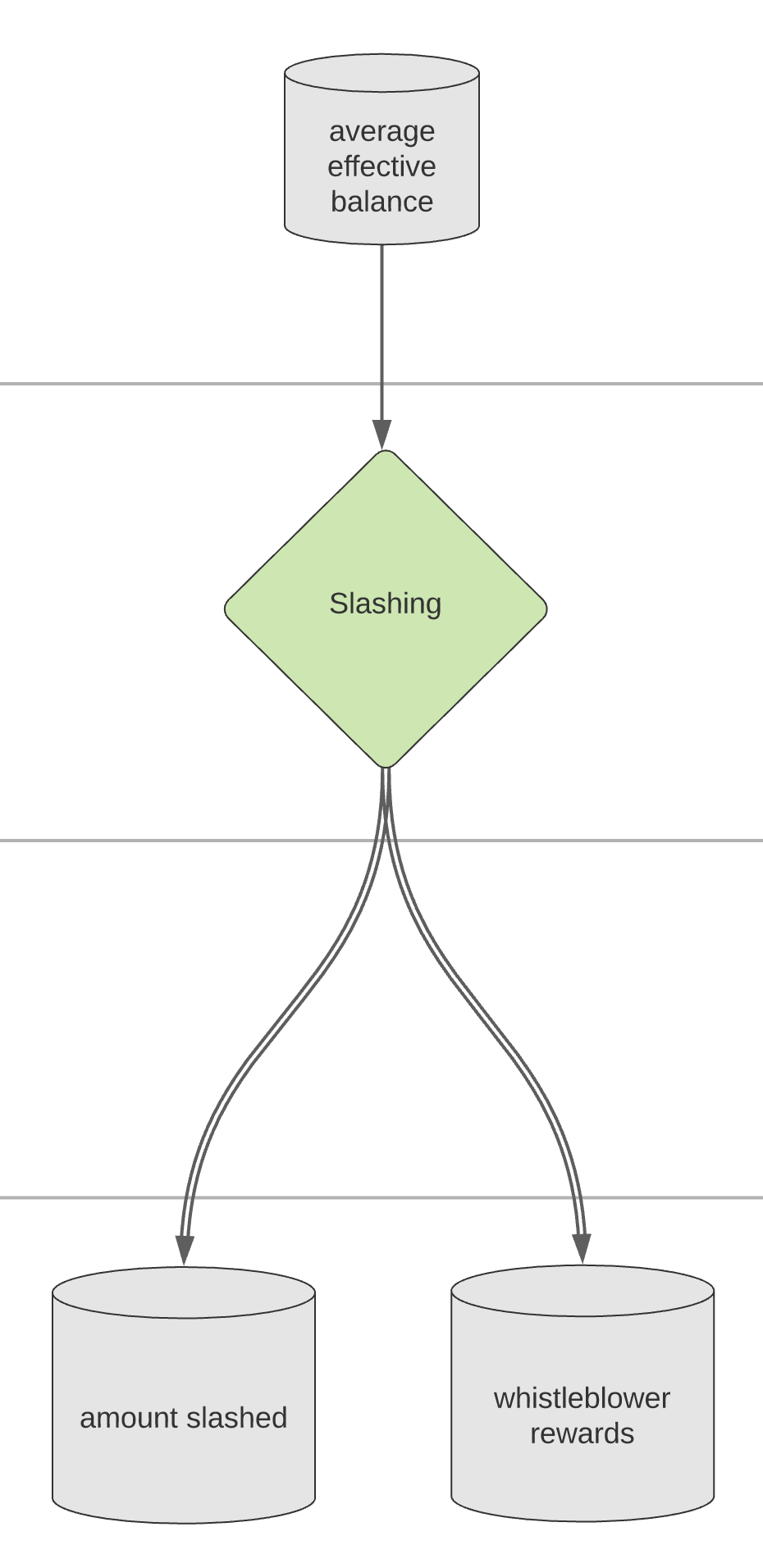
PSUB 9: Slashing Rewards & Penalties#

First, we calculate the slashing reward for a single slashing event, indicated by $'$:

(10)#\[\begin{equation} \begin{aligned} \psi' &= \frac{\bar{B}}{\text{MIN_SLASHING_PENALTY_QUOTIENT}}\\ \end{aligned} \end{equation}\]

The whistleblower rewards are made up of both a reward for the whistleblower, and for the proposer:

(11)#\[\begin{equation} \begin{aligned} R'_w &= \frac{\bar{B}}{\text{WHISTLEBLOWER_REWARD_QUOTIENT}} \qquad &(\text{reward for whistleblower})\\ &+ \psi' \times \frac{\text{PROPOSER_WEIGHT}}{\text{WEIGHT_DENOMINATOR}} \qquad &(\text{reward for proposer}\\ &&\text{who includes slashing})\\ \end{aligned} \end{equation}\]

In addition to the slashing penalty, there is a slashing penalty proportional to the total slashings in the current time period using the PROPORTIONAL_SLASHING_MULTIPLIER:

(12)#\[\begin{equation} \begin{aligned} N &= \frac{\text{slashing_events_per_1000_epochs}}{1000} \qquad (\text{slashing events in epoch})\\ \psi'_{proportional} &= \frac{\bar{B}}{\text{EFFECTIVE_BALANCE_INCREMENT}}\\ &\times min(\psi' \times N \times \text{PROPORTIONAL_SLASHING_MULTIPLIER},X)\\ &\times \frac{\text{EFFECTIVE_BALANCE_INCREMENT}}{X} \end{aligned} \end{equation}\]

Finally, the individual slashing penalty is calculated as the sum of the individual slashing and proportional slashing penalties:

\[ \psi' = \psi' + \psi'_{proportional} \]

To calculate the total amount slashed and whistleblower rewards for the epoch, we scale by the number of slashing events per epoch:

(13)#\[\begin{equation} \begin{aligned} \psi &= \psi' \times N\\ R_w &= R'_w \times N\\ \end{aligned} \end{equation}\]

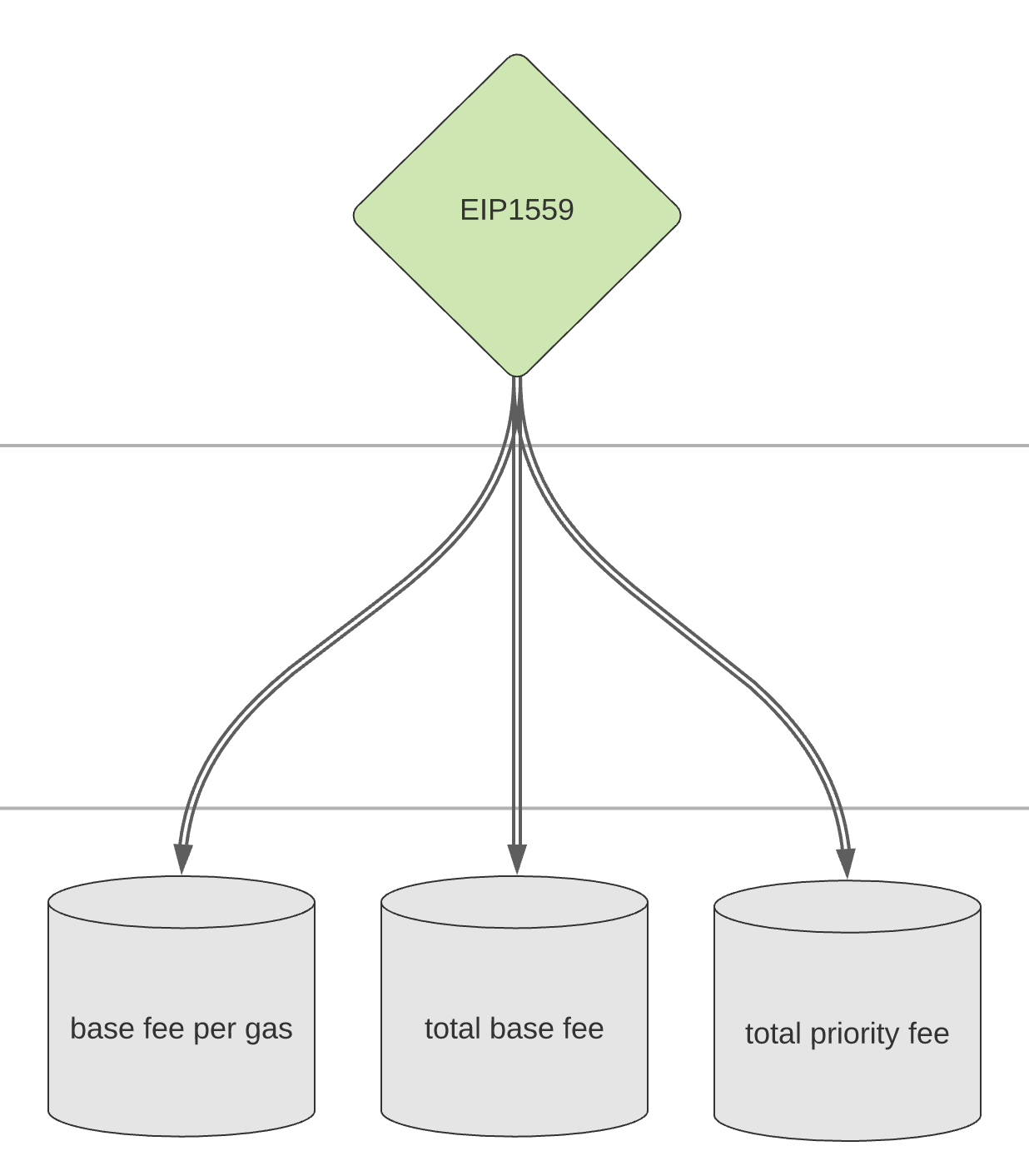
PSUB 10: EIP1559 Transaction Pricing#

EIP-1559 replaces the current transaction gas price (in Gwei per gas), with two values: a dynamic base fee that is burned and applied to all transactions, and a priority fee per transaction that is paid to miners/validators.

The current gas limit is replaced by two values:

a “long-term average target” equal to the current gas limit
a “hard per-block cap” which is twice the current gas limit

The long-term average gas target per block is set to 15m gas; by default we assume the gas used per block will on average be equal to the gas target.

Pre-merge, while Proof-of-Work is still active, miners receive the priority fee, and the gas used is calculated according to block-time:

(14)#\[\begin{equation} \begin{aligned} \text{gas used} &= \text{blocks per epoch} \times \text{gas target}\\ F &= \text{gas used} \times f\\ T = T_m &= \text{gas used} \times t\\ \end{aligned} \end{equation}\]

Post-merge, when Proof-of-Work is deprecated and Proof-of-Stake validators start including transactions, validators receive the priority fee, and the gas used is calculated according to slot-time:

(15)#\[\begin{equation} \begin{aligned} \text{gas used} &= \text{slots per epoch} \times \text{gas target}\\ F &= \text{gas used} \times f\\ T = T_v &= \text{gas used} \times t\\ \end{aligned} \end{equation}\]

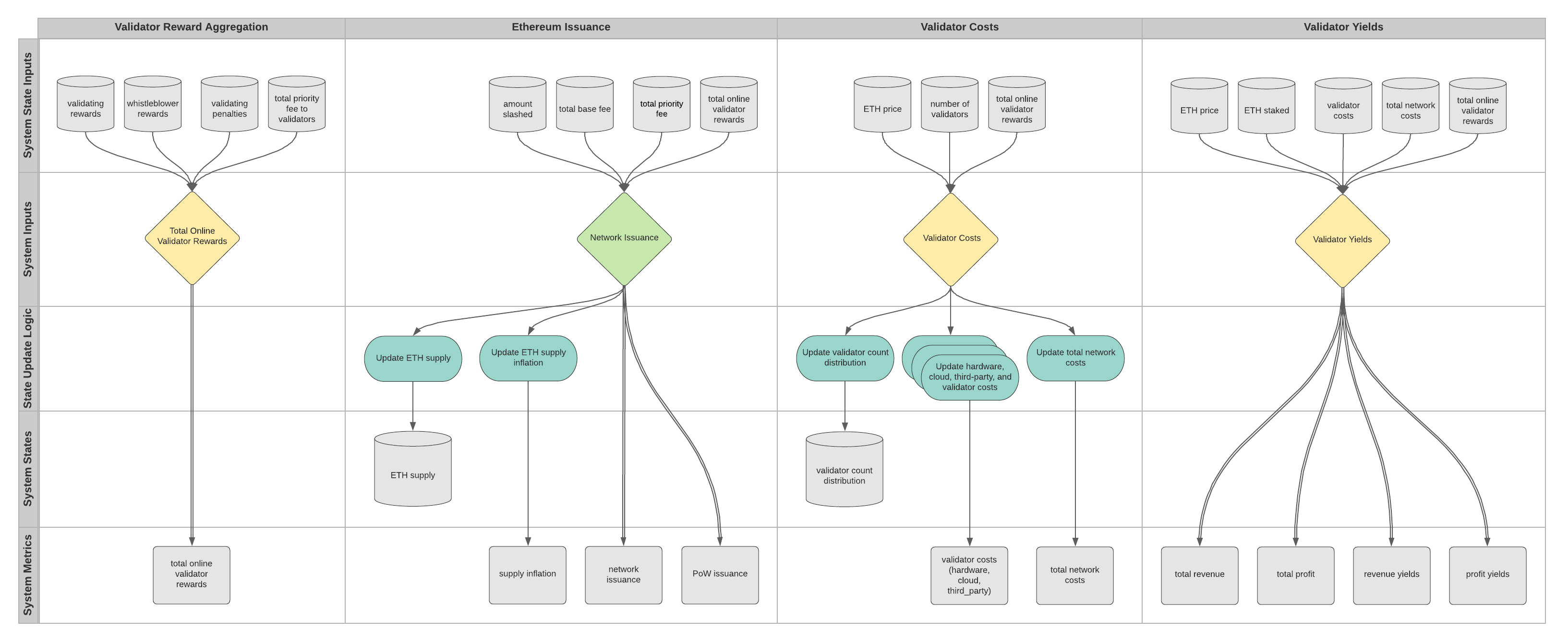
System Metrics#

System Metrics are computed from State Variables in order to assess the performance of the system. The calculation of our System Metrics is also represented in the model’s cadCAD Canvas / Differential Model Specification and accessible via LucidChart. Below is an illustrative screenshot.

The following state-update logic for system metric State Variables could also be performed in post-processing, assuming there are no feedback loops that influence the metrics, to improve run-time performance.

Validator Reward Aggregation#

The total online validator rewards is the net rewards and penalties awarded to online validators accounting for validating, whistleblowing, and priority fees post-merge:

\[ R_o = R_v + R_w + T - Z \]

Ethereum Issuance#

The ETH supply at the next epoch is equal to the sum of the ETH supply at the current epoch and the net network issuance:

\[ S^+ = S + (R_v + R_w - Z - \psi - F) \]

Validator Costs#

The validator costs is the sum of hardware, cloud, and third-party costs per validator type:

\[ \vec{C} = \vec{C}_{hardware} + \vec{C}_{cloud} + \vec{C}_{third-party} \qquad ([$]) \]

The total network costs is the sum of validator costs over all validator types (row index $i$):

\[ C = \sum_{i}{\vec{C}_{ij}} \qquad ($) \]

Validator Revenue and Profit#

The validator revenue is the rewards for online validators in ETH, $R_o / 10^9$, distributed according to the validator percentage distribution multiplied by the current ETH price $P$:

\[ \vec{K}_r = \text{validator_percentage_distribution} \times R_o / 10^9 \times P \qquad ([$]) \]

The validator profit is the validator revenue less the validator costs:

\[ \vec{K}_p = \vec{K}_r - \vec{C} \qquad ([$]) \]

The total revenue is the sum of validator revenue over all validator types:

\[ K_r = \sum_{i}{\vec{K}_{r,ij}} \qquad ($) \]

The total profit is the total revenue less the total network costs:

\[ K_p = K_r - C \qquad ($) \]

Validator Revenue and Profit Yields#

The per-validator revenue and profit yields are calculated and annualized as the validator profit and revenue multiplied by the number of epochs in a year divided by the validator ETH staked, $\sigma$, in dollars:

\[\vec{Y}_r = \frac{\vec{K}_r \times E_{year}}{\sigma \times P} \qquad ([\%])\]

\[\vec{Y}_p = \frac{\vec{K}_p \times E_{year}}{\sigma \times P} \qquad ([\%])\]

The total revenue and profit yields are calculated and annualized as the total profit and revenue multiplied by the number of epochs in a year divided by the total ETH staked, $X$, in dollars:

\[Y_r = \frac{K_r \times E_{year}}{X \times P} \qquad (\%)\]

\[Y_p = \frac{K_p \times E_{year}}{X \times P} \qquad (\%)\]

Name	Symbol	Domain	Unit	Variable
Base Reward	\(\beta\)	\(\mathbb{R}^+\)	\(\text{Gwei}\)	`base_reward`
Source Reward	\(r_s\)	\(\mathbb{R}^+\)	\(\text{Gwei}\)	`source_reward`
Target Reward	\(r_t\)	\(\mathbb{R}^+\)	\(\text{Gwei}\)	`target_reward`
Head Reward	\(r_h\)	\(\mathbb{R}^+\)	\(\text{Gwei}\)	`head_reward`
Block Proposer Reward	\(r_p\)	\(\mathbb{R}^+\)	\(\text{Gwei}\)	`block_proposer_reward`
Sync Reward	\(r_{sync}\)	\(\mathbb{R}^+\)	\(\text{Gwei}\)	`sync_reward`
Amount Slashed	\(\psi\)	\(\mathbb{R}^+\)	\(\text{Gwei}\)	`amount_slashed`
Validating Rewards	\(R_v\)	\(\mathbb{R}^+\)	\(\text{Gwei}\)	`validating_rewards`
Whistleblower Rewards	\(R_w\)	\(\mathbb{R}^+\)	\(\text{Gwei}\)	`whistleblower_rewards`
Attestation Penalties	\(Z_a\)	\(\mathbb{R}^+\)	\(\text{Gwei}\)	`attestation_penalties`
Sync Committee Penalties	\(Z_{sync}\)	\(\mathbb{R}^+\)	\(\text{Gwei}\)	`sync_committee_penalties`
Validating Penalties	\(Z\)	\(\mathbb{R}^+\)	\(\text{Gwei}\)	`validating_penalties`
Total Online Validator Rewards	\(R_o\)	\(\mathbb{R}^+\)	\(\text{Gwei}\)	`total_online_validator_rewards`

Name	Symbol	Domain	Unit	Variable	Description
ETH Price	\(P\)	\(\mathbb{R}^+\)	\(/\text{ETH}\)	`eth_price`	ETH spot price sample (from exogenous process)
ETH Supply	\(S\)	\(\mathbb{R}^+\)	\(\text{ETH}\)	`eth_supply`	ETH supply with inflation/deflation
ETH Staked	\(X\)	\(\mathbb{R}^+\)	\(\text{ETH}\)	`eth_staked`	Total ETH staked (“active balance”) by all active validators

Name	Symbol	Domain	Unit	Variable
# Validators in Activation Queue	\(V_{queue}\)	\(\mathbb{R}^+\)	None	`number_of_validators_in_activation_queue`
# Validators	\(V\)	\(\mathbb{R}^+\)	None	`number_of_validators`
# Validators Online	\(V_{online}\)	\(\mathbb{R}^+\)	None	`number_of_validators_online`
# Validators Offline	\(V_{offline}\)	\(\mathbb{R}^+\)	None	`number_of_validators_offline`
Average Effective Balance	\(\bar{B}\)	\(\mathbb{R}^+\)	\(\text{Gwei}\)	`average_effective_balance`
Validator ETH Staked	\(\vec{\sigma}\)	\(\mathbb{R}^+\)	\([\text{ETH}]\)	`validator_eth_staked`

Name	Symbol	Domain	Unit	Variable
Base Fee per Gas	\(f\)	\(\mathbb{R}^+\)	\(\text{Gwei/gas}\)	`base_fee_per_gas`
Total Base Fee	\(F\)	\(\mathbb{R}^+\)	\(\text{Gwei}\)	`total_base_fee`
Priority Fee per Gas	\(t\)	\(\mathbb{R}^+\)	\(\text{Gwei/gas}\)	`base_fee_per_gas`
Total Priority Fee to Validators	\(T_v\)	\(\mathbb{R}^+\)	\(\text{Gwei}\)	`total_priority_fee_to_validators`
Total Priority Fee to Miners	\(T_m\)	\(\mathbb{R}^+\)	\(\text{Gwei}\)	`total_priority_fee_to_miners`

Name	Symbol	Domain	Unit	Variable
Validator Revenue	\(\vec{K_r}\)	\(\mathbb{R}\)	[$]	`validator_revenue`
Validator Profit	\(\vec{K_p}\)	\(\mathbb{R}\)	[$]	`validator_profit`
Validator Revenue Yields	\(\vec{Y_r}\)	\(\mathbb{R}\)	\([\%]\)	`validator_revenue_yields`
Validator Profit Yields	\(\vec{Y_p}\)	\(\mathbb{R}\)	\([\%]\)	`validator_profit_yields`
Validator Count Distribution	\(\vec{V}\)	\(\mathbb{R}^+\)	\([\%]\)	`validator_count_distribution`
Validator Hardware Costs	\(\vec{C}_{hardware}\)	\(\mathbb{R}^+\)	[$]	`validator_hardware_costs`
Validator Cloud Costs	\(\vec{C}_{cloud}\)	\(\mathbb{R}^+\)	[$]	`validator_cloud_costs`
Validator Third-Party Costs	\(\vec{C}_{third-party}\)	\(\mathbb{R}^+\)	\([\%]\)	`validator_third_party_costs`
Validator Costs	\(\vec{C}\)	\(\mathbb{R}^+\)	[$]	`validator_costs`

Name	Symbol	Domain	Unit	Variable
ETH Supply Inflation	\(I\)	\(\mathbb{R}\)	\(\%\)	`supply_inflation`
Total Revenue	\(K_r\)	\(\mathbb{R}\)	$	`total_revenue`
Total Profit	\(K_p\)	\(\mathbb{R}\)	$	`total_profit`
Total Network Costs	\(C\)	\(\mathbb{R}^+\)	$	`total_network_costs`
Total Revenue Yields	\(Y_r\)	\(\mathbb{R}\)	\(\%\)	`total_revenue_yields`
Total Profit Yields	\(Y_p\)	\(\mathbb{R}\)	\(\%\)	`total_profit_yields`

Variable	Unit	Description
`validator_percentage_distribution`	\(\begin{bmatrix} \% \end{bmatrix}\)	The distribution of the total number of validators per validator type. Vector sum is a total of 100%.
`validator_hardware_costs_per_epoch`	\(\begin{bmatrix} USD \end{bmatrix}\)	The per-epoch costs for DIY hardware infrastructure per validator type
`validator_cloud_costs_per_epoch`	\(\begin{bmatrix} USD \end{bmatrix}\)	The per-epoch costs for cloud computing resources per validator type
`validator_third_party_costs_per_epoch`	\(\begin{bmatrix} \% \end{bmatrix}\)	A percentage value of the total validator rewards that goes to third-party service providers as a fee per validator type

Name	Symbol	Domain	Unit	Variable	Value
Epochs per year	\(E_{year}\)	\(\mathbb{Z}^+\)	\(\text{epochs}\)	`epochs_per_year`	82180
Epochs per day	\(E_{day}\)	\(\mathbb{Z}^+\)	\(\text{epochs}\)	`epochs_per_day`	225